Relasi
Relasi adalah suatu aturan yang memasangkan anggota himpunan satu ke himpunan lain. Suatu relasi dari himpunan A ke himpunan B adalah pemasangan atau korespondensi dari anggota-anggota himpunan A ke anggota-anggota himpunan B.Jika diketahui himpunan A = {1, 2, 3, 4} dan B = {4, 5, 6, 7}, maka relasi “tiga kurangnya dari” himpunan A ke himpunan B dapat disajikan dalam diagram panah, diagram Cartesius, himpunan pasangan berurutan, dan dengan rumus.
a. Diagram panah
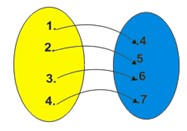
b. Diagram Cartesius
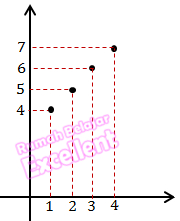
c. Himpunan pasangan berurutan
R = {(1,4), (2,5), (3,6), (4, 7)}
d. Dengan rumus
Relasi antara anggota himpunan A dan B dapat dinyatakan dengan menggunakan rumus. Misalnya anggota A dinyatakan dengan x, maka pasangannya, yaitu y merupakan anggota B, dirumuskan:
y = x + 3
atau dapat pula dinyatakan dalam bentuk
f(x) = x + 3, di mana x ∈ {1, 2, 3, 4}
Fungsi
Pengertian FungsiSuatu relasi dari himpunan A ke himpunan B disebut fungsi dari A ke B jika setiap anggota A dipasangkan dengan tepat satu anggota B.
Perhatikan diagram panah berikut.
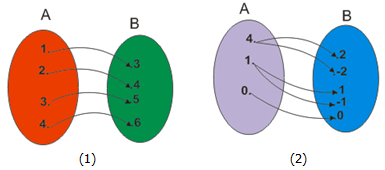
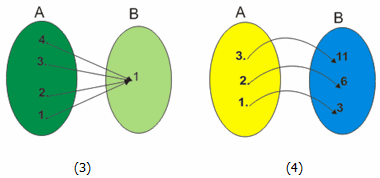
Pada gambar (1), (3) dan (4) di atas, setiap anggota himpunan A mempunyai pasangan tepat satu anggota himpunan B. Relasi yang memiliki ciri seperti itu disebut fungsi atau pemetaan. Sedangkan gambar (2) bukan fungsi karena ada anggota A yang punya pasangan lebih dari satu anggota B.
Jika f adalah suatu fungsi dari A ke B, maka:
- himpunan A disebut domain (daerah asal),
- himpunan B disebut kodomain (daerah kawan) dan
- himpunan C, yaitu anggota B yang berpasangan dengan himpunan A disebut range (hasil) fungsi f.
Untuk lebih memahami tentang fungsi, pelajarilah contoh soal berikut.
Diketahui A = {1, 2, 3, 4} dan B = {1, 2, 3, 4, 5, 6, 7, 8}.
Suatu fungsi f : A→B ditentukan oleh f(x) = 2x – 1.
1. Gambarlah fungsi f dengan diagram panah.
2. Tentukan domain, kodomain dan range fungsi f.
3. Gambarlah grafik fungsi f.
Penyelesaian:
Diketahui A = {1, 2, 3, 4}
f(x) = 2x – 1
x = 1 → f(1) = 2(1) – 1 = 1
x = 2 → f(2) = 2(2) – 1 = 3
x = 3 → f(3) = 2(3) – 1 = 5
x = 4 → f(4) = 2(4) – 1 = 7
a. Diagram Panah
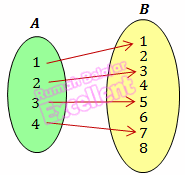
b. Dari diagram di atas terlihat bahwa
Domain: {1, 2, 3, 4}
Kodomain: {1, 2, 3, 4, 5, 6, 7, 8}
Range: {1, 3, 5, 7}
c. Grafik fungsi
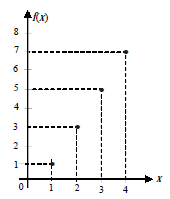
















0 comments:
Post a Comment