Macam-Macam Fungsi

1) Fungsi konstan (fungsi tetap)

Suatu fungsi f : A → B ditentukan dengan rumus f(x) disebut fungsi konstan apabila untuk setiap anggota domain fungsi selalu berlaku f(x) = C, di mana C bilangan konstan. Untuk lebih jelasnya, pelajarilah contoh soal berikut ini.
Contoh soal
Diketahui f : R → R dengan rumus f(x) = 2 dengan daerah domain: {x | –2 ≤ x < 5}. Tentukan gambar grafiknya. Penyelesaian
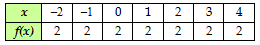
Grafik:

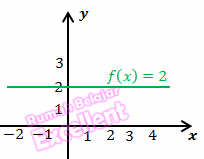
2) Fungsi linear

Suatu fungsi f(x) disebut fungsi linear apabila fungsi itu ditentukan oleh f(x) = ax + b, di mana a ≠ 0, a dan b bilangan konstan dan grafiknya berupa garis lurus.
Pelajarilah contoh soal berikut ini agar kamu lebih jelas memahami fungsi linear.
Contoh soal
Jika diketahui f(x) = 2x + 3, gambarlah grafiknya.
Penyelesaian:

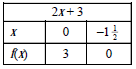
Grafik

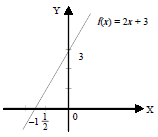
3) Fungsi identitas

Suatu fungsi f(x) disebut fungsi identitas apabila setiap anggota domain fungsi berlaku f(x) = x atau setiap anggota domain fungsi dipetakan pada dirinya sendiri.
Grafik fungsi identitas berupa garis lurus yang melalui titik asal dan semua titik absis maupun ordinatnya sama. Fungsi identitas ditentukan oleh f(x) = x.

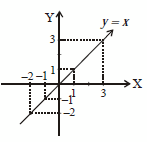
4) Fungsi kuadrat

Suatu fungsi f(x) disebut fungsi kuadrat apabila fungsi itu ditentukan oleh f(x) = ax² + bx + c, di mana a ≠ 0 dan a, b, dan c bilangan konstan dan grafiknya berupa parabola.

5) Fungsi tangga (bertingkat)

Suatu fungsi f(x) disebut fungsi tangga apabila grafik fungsi f(x) berbentuk interval-interval yang sejajar.
Contoh

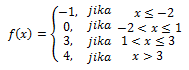
Grafiknya

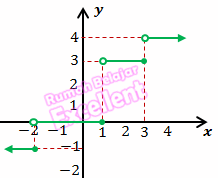
6) Fungsi Mutlak (modulus)

Suatu fungsi f(x) disebut fungsi modulus (mutlak) apabila fungsi ini memetakan setiap bilangan real pada domain fungsi ke unsur harga mutlaknya.
f : x → | x | atau f : x → | ax + b |
f(x) = | x | artinya:

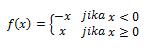
Grafiknya

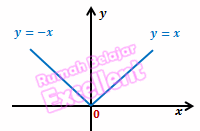
7) Fungsi ganjil dan fungsi genap

Suatu fungsi f(x) disebut fungsi ganjil apabila berlaku f(–x) = –f(x) dan disebut fungsi genap apabila berlaku f(–x) = f(x). Jika f(–x) ≠ –f(x) maka fungsi ini bukan genap dan bukan ganjil. Untuk memahami fungsi ganjil dan fungsi genap, perhatikan contoh soal berikut ini.
Contoh soal
Tentukan fungsi f di bawah ini termasuk fungsi genap, fungsi ganjil, atau tidak genap dan tidak ganjil.
1. f(x) = 6x³ + x
2. f(x) = cos x + 2
3. f(x) = 3x² – x
Penyelesaian
1. f(x) = 6x³ + x

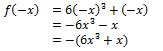
Jadi, fungsi f(x) merupakan fungsi ganjil.
2. f(x) = cos x + 2

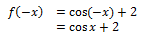
f(x) = –f(x)
Jadi, fungsi f(x) merupakan fungsi genap.
3. f(x) = 3x² – x

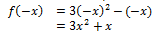
Fungsi f(–x) ≠ f(x) dan f(–x) ≠ –f(x).
Jadi, fungsi f(x) adalah tidak genap dan tidak ganjil.

selain fungsi-fungsi di atas masih ada beberapa fungsi yang lain, namun pembahasan kami hari ini cukup sekian dulu. Semoga bermanfaat

Posted in: 11 SMA IPA,Komposisi Fungsi,Matematika