Pada bagian sebelumnya, Anda telah belajar menentukan fungsi komposisi f o g atau g o f jika fungsi f dan g diketahui. Bagaimana jika terjadi sebaliknya? Fungsi yang diketahui adalah fungsi komposisi f o g atau g o f dan salah satu fungsi yang membentuk komposisi fungsi tersebut, bagaimana cara menentukan fungsi lainnya?
Perhatikan contoh berikut:
Contoh 1
Diketahui f(x) = x – 3 dan (f o g)(x) = 5x – 3. Tentukan fungsi g(x)
Penyelesaian:
| (f o g)(x) | = 5x – 3 |
| f(g(x)) | = 5x – 3 |
| g(x) – 3 | = 5x – 3 |
| g(x) | = 5x |
Contoh 2
Diketahui f:R→R dan g:R→R ditentukan oleh f(x) = x + 3 dan (f o g)(x) = x2 + 6x + 7, maka tentukan g(x) !
Penyelesaian:
| (f o g)(x) | = x2 + 6x + 7 |
| f(g(x)) | = x2 + 6x + 7 |
| g(x) + 3 | = x2 + 6x + 7 |
| g(x) | = x2 + 6x + 4 |
Contoh3
Diketahui f(x) = x2 + 2x + 5 dan (f o g)(x) = 4x2 + 20 x + 29. Tentukan fungsi g(x)
Penyelesaian:
| (f o g)(x) | = 4x2 + 20 x + 29 |
| f(g(x)) | = 4x2 + 20 x + 29 |
| [g(x)]2 + 2[g(x)]+5 | = 4x2 + 20 x + 29 |
| [g(x)]2 + 2[g(x)] + 1 + 4 | = 4x2 + 20 x + 29 |
| [g(x) + 1]2 + 4 | = 4x2 + 20 x + 29 |
| [g(x) + 1]2 | = 4x2 + 20 x + 25 |
| [g(x) + 1]2 | = (2x + 5)2 |
| g(x) + 1 | = 2x + 5 |
| g(x) | = 2x + 4 |
Contoh 4
Diketahui g(x) = 2x + 4 dan (f o g)(x) = 4x2 + 20 x + 29. Tentukan fungsi f(x)
Penyelesaian:
| (f o g)(x) | = 4x2 + 20 x + 29 |
| f(g(x)) | = 4x2 + 20 x + 29 |
| f(2x+4) | = (4x2 + 16x + 29) + 4x + 8 + 5 |
| f(2x+4) | = (2x + 4)2 + 2(2x + 4) + 5 |
| f(x) | = x2 + 2x + 5 |
Cara Lain:
Dengan Menentukan Fungsi Invers dari g(x) = 2x + 4 kemudian mensubtitusikannya kedalam nilai x pada (f o g)(x) = 4x2 + 20 x + 29.
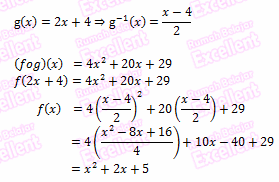
















2 comments:
sangat membantu,sankyu :D (Y)
👍👍👍thanks!
Post a Comment