Wednesday, November 20, 2013
Wednesday, November 13, 2013
Fungsi Invers
Definisi Fungsi Invers
Jika fungsi f : A→B dinyatakan dengan pasangan terurut f = {(x,y) |y=f(x), x∈A dan y∈B}
Maka relaasi fungsi g : B → A dinyatakan dengan pasangan terurut g = {(x,y) |x=g(y), x∈A dan y∈B} dinamakan invers fungsi f ditulis f -1
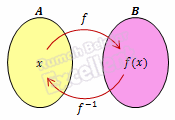
Untuk menentukan fungsi invers dari suatu fungsi dapat dilakukan dengan cara berikut ini.
a. Buatlah permisalan f(x) = y pada persamaan.
b. Nyatakanlah Persamaan tersebut dalam x = f(y).
c. Gantilah y dengan x, sehingga f(y) = f -1(x).
Contoh 1
Tentukan fungsi invers dari f(x) = x + 12
Penyelesaian:
Dengan demikian f -1(x)= x – 12
Contoh 2
Tentukan fungsi invers dari fungsi
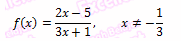
Penyelesaian:
misalkan y = f(x) sehingga
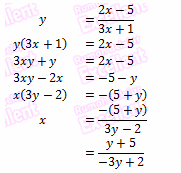
Berikut ini beberapa Rumus PRAKTIS yang dapat digunakan untuk menentukan Invers suatu fungsi

Jika fungsi f : A→B dinyatakan dengan pasangan terurut f = {(x,y) |y=f(x), x∈A dan y∈B}
Maka relaasi fungsi g : B → A dinyatakan dengan pasangan terurut g = {(x,y) |x=g(y), x∈A dan y∈B} dinamakan invers fungsi f ditulis f -1

Untuk menentukan fungsi invers dari suatu fungsi dapat dilakukan dengan cara berikut ini.
a. Buatlah permisalan f(x) = y pada persamaan.
b. Nyatakanlah Persamaan tersebut dalam x = f(y).
c. Gantilah y dengan x, sehingga f(y) = f -1(x).
Contoh 1
Tentukan fungsi invers dari f(x) = x + 12
Penyelesaian:
| y | = f (x) |
| y | = x + 12 |
| x | = y – 12 |
Contoh 2
Tentukan fungsi invers dari fungsi
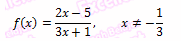
Penyelesaian:
misalkan y = f(x) sehingga
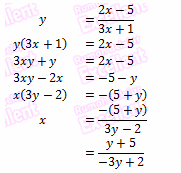
Berikut ini beberapa Rumus PRAKTIS yang dapat digunakan untuk menentukan Invers suatu fungsi

Menentukan Fungsi f atau g jika diketahui Fungsi Komposisi dari f atau g
Pada bagian sebelumnya, Anda telah belajar menentukan fungsi komposisi f o g atau g o f jika fungsi f dan g diketahui. Bagaimana jika terjadi sebaliknya? Fungsi yang diketahui adalah fungsi komposisi f o g atau g o f dan salah satu fungsi yang membentuk komposisi fungsi tersebut, bagaimana cara menentukan fungsi lainnya?
Perhatikan contoh berikut:
Contoh 1
Diketahui f(x) = x – 3 dan (f o g)(x) = 5x – 3. Tentukan fungsi g(x)
Penyelesaian:
Contoh 2
Diketahui f:R→R dan g:R→R ditentukan oleh f(x) = x + 3 dan (f o g)(x) = x2 + 6x + 7, maka tentukan g(x) !
Penyelesaian:
Contoh3
Diketahui f(x) = x2 + 2x + 5 dan (f o g)(x) = 4x2 + 20 x + 29. Tentukan fungsi g(x)
Penyelesaian:
Contoh 4
Diketahui g(x) = 2x + 4 dan (f o g)(x) = 4x2 + 20 x + 29. Tentukan fungsi f(x)
Penyelesaian:
Cara Lain:
Dengan Menentukan Fungsi Invers dari g(x) = 2x + 4 kemudian mensubtitusikannya kedalam nilai x pada (f o g)(x) = 4x2 + 20 x + 29.
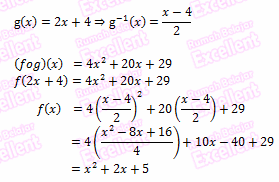
Perhatikan contoh berikut:
Contoh 1
Diketahui f(x) = x – 3 dan (f o g)(x) = 5x – 3. Tentukan fungsi g(x)
Penyelesaian:
| (f o g)(x) | = 5x – 3 |
| f(g(x)) | = 5x – 3 |
| g(x) – 3 | = 5x – 3 |
| g(x) | = 5x |
Contoh 2
Diketahui f:R→R dan g:R→R ditentukan oleh f(x) = x + 3 dan (f o g)(x) = x2 + 6x + 7, maka tentukan g(x) !
Penyelesaian:
| (f o g)(x) | = x2 + 6x + 7 |
| f(g(x)) | = x2 + 6x + 7 |
| g(x) + 3 | = x2 + 6x + 7 |
| g(x) | = x2 + 6x + 4 |
Contoh3
Diketahui f(x) = x2 + 2x + 5 dan (f o g)(x) = 4x2 + 20 x + 29. Tentukan fungsi g(x)
Penyelesaian:
| (f o g)(x) | = 4x2 + 20 x + 29 |
| f(g(x)) | = 4x2 + 20 x + 29 |
| [g(x)]2 + 2[g(x)]+5 | = 4x2 + 20 x + 29 |
| [g(x)]2 + 2[g(x)] + 1 + 4 | = 4x2 + 20 x + 29 |
| [g(x) + 1]2 + 4 | = 4x2 + 20 x + 29 |
| [g(x) + 1]2 | = 4x2 + 20 x + 25 |
| [g(x) + 1]2 | = (2x + 5)2 |
| g(x) + 1 | = 2x + 5 |
| g(x) | = 2x + 4 |
Contoh 4
Diketahui g(x) = 2x + 4 dan (f o g)(x) = 4x2 + 20 x + 29. Tentukan fungsi f(x)
Penyelesaian:
| (f o g)(x) | = 4x2 + 20 x + 29 |
| f(g(x)) | = 4x2 + 20 x + 29 |
| f(2x+4) | = (4x2 + 16x + 29) + 4x + 8 + 5 |
| f(2x+4) | = (2x + 4)2 + 2(2x + 4) + 5 |
| f(x) | = x2 + 2x + 5 |
Cara Lain:
Dengan Menentukan Fungsi Invers dari g(x) = 2x + 4 kemudian mensubtitusikannya kedalam nilai x pada (f o g)(x) = 4x2 + 20 x + 29.
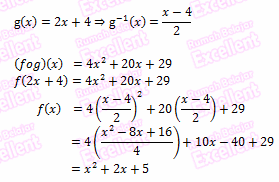
Monday, November 11, 2013
Komposisi Fungsi (bagian I)
komposisi dan dilambangkan dengan "o" dibaca "bundaran" atau "komposisi"
untuk gof dibaca “fungsi g bundaran f”.
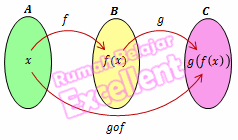
fungsi dari A ke C pada gambar diatas disebut fungsi komposisi dari g dan f ditulis gof.
Perhatikan bahwa dalam fungsi komposisi (gof)(x)=g(f(x)) ditentukan dengan pengerjaan f(x) terlebih dahulu kemudian dilanjutkan dengan pengerjaan oleh g(x)
Sedangkan, untuk fog dibaca "fungsi f bundaran g".
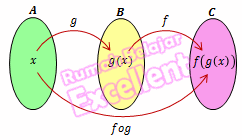
fungsi dari A ke C pada gambar disebut fungsi komposisi dari f dan g ditulis fog.
Fungsi komposisi (fog)(x)=f(g(x)) ditentukan dengan pengerjaan g(x) terlebih dahulu kemudian dilanjutkan dengan pengerjaan oleh f(x)
Contoh 1
Diketahui f(x) = 3x + 2, g(x) = x2 + 1.
a. Tentukan (g o f)(x).
b. Tentukan (f o g)(x).
c. Apakah berlaku sifat komutatif: g o f = f o g?
Penyelesaian
a. f(x) = 3x + 2 dan g(x) = x2 + 1
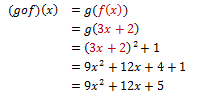
b. g(x) = x2 + 1 dan f(x) = 3x + 2
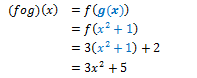
c. Dari penyelesaian diatas, tampak bahwa g o f ≠ f o g, sehingga tidak berlaku sifat komutatif
untuk gof dibaca “fungsi g bundaran f”.

fungsi dari A ke C pada gambar diatas disebut fungsi komposisi dari g dan f ditulis gof.
Perhatikan bahwa dalam fungsi komposisi (gof)(x)=g(f(x)) ditentukan dengan pengerjaan f(x) terlebih dahulu kemudian dilanjutkan dengan pengerjaan oleh g(x)
Sedangkan, untuk fog dibaca "fungsi f bundaran g".

fungsi dari A ke C pada gambar disebut fungsi komposisi dari f dan g ditulis fog.
Fungsi komposisi (fog)(x)=f(g(x)) ditentukan dengan pengerjaan g(x) terlebih dahulu kemudian dilanjutkan dengan pengerjaan oleh f(x)
Contoh 1
Diketahui f(x) = 3x + 2, g(x) = x2 + 1.
a. Tentukan (g o f)(x).
b. Tentukan (f o g)(x).
c. Apakah berlaku sifat komutatif: g o f = f o g?
Penyelesaian
a. f(x) = 3x + 2 dan g(x) = x2 + 1
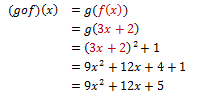
b. g(x) = x2 + 1 dan f(x) = 3x + 2
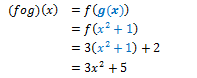
c. Dari penyelesaian diatas, tampak bahwa g o f ≠ f o g, sehingga tidak berlaku sifat komutatif
Sifat-Sifat Fungsi
1. Fungsi injektif (satu-satu)
Jika fungsi f : A → B, setiap b ∈ B hanya mempunyai satu kawan saja di A, maka fungsi itu disebut fungsi satu-satu atau injektif.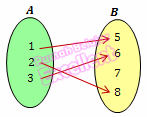
Fungsi injektif
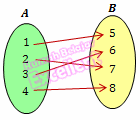
Fungsi injektif
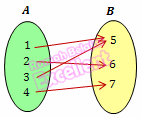
Fungsi injektif
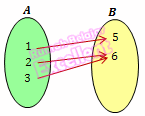
bukan fungsi injektif
2. Fungsi surjektif (onto)
Pada fungsi f : A → B, setiap b ∈ B mempunyai kawan di A, maka f disebut fungsi surjektif atau onto.
Fungsi surjektif

Bukan fungsi surjektif
3. Fungsi bijektif (korespondensi satu-satu)
Suatu fungsi yang bersifat injektif sekaligus surjektif disebut fungsi bijektif atau korespondensi satu-satu.
Korespondensi satu-satu

Bukan korespodensi satu-satu
Macam-Macam Fungsi
1) Fungsi konstan (fungsi tetap)
Suatu fungsi f : A → B ditentukan dengan rumus f(x) disebut fungsi konstan apabila untuk setiap anggota domain fungsi selalu berlaku f(x) = C, di mana C bilangan konstan. Untuk lebih jelasnya, pelajarilah contoh soal berikut ini.Contoh soal
Diketahui f : R → R dengan rumus f(x) = 2 dengan daerah domain: {x | –2 ≤ x < 5}. Tentukan gambar grafiknya. Penyelesaian
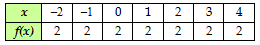
Grafik:
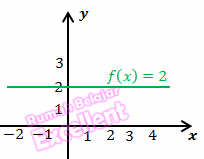
2) Fungsi linear
Suatu fungsi f(x) disebut fungsi linear apabila fungsi itu ditentukan oleh f(x) = ax + b, di mana a ≠ 0, a dan b bilangan konstan dan grafiknya berupa garis lurus.Pelajarilah contoh soal berikut ini agar kamu lebih jelas memahami fungsi linear.
Contoh soal
Jika diketahui f(x) = 2x + 3, gambarlah grafiknya.
Penyelesaian:
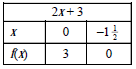
Grafik
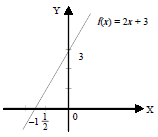
3) Fungsi identitas
Suatu fungsi f(x) disebut fungsi identitas apabila setiap anggota domain fungsi berlaku f(x) = x atau setiap anggota domain fungsi dipetakan pada dirinya sendiri.Grafik fungsi identitas berupa garis lurus yang melalui titik asal dan semua titik absis maupun ordinatnya sama. Fungsi identitas ditentukan oleh f(x) = x.
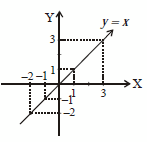
4) Fungsi kuadrat
Suatu fungsi f(x) disebut fungsi kuadrat apabila fungsi itu ditentukan oleh f(x) = ax2 + bx + c, di mana a ≠ 0 dan a, b, dan c bilangan konstan dan grafiknya berupa parabola.5) Fungsi tangga (bertingkat)
Suatu fungsi f(x) disebut fungsi tangga apabila grafik fungsi f(x) berbentuk interval-interval yang sejajar.Contoh
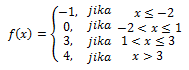
Grafiknya
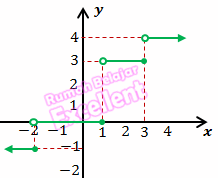
6) Fungsi Mutlak (modulus)
Suatu fungsi f(x) disebut fungsi modulus (mutlak) apabila fungsi ini memetakan setiap bilangan real pada domain fungsi ke unsur harga mutlaknya.f : x → | x | atau f : x → | ax + b |
f(x) = | x | artinya:
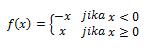
Grafiknya
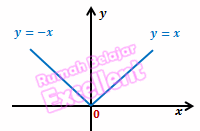
7) Fungsi ganjil dan fungsi genap
Suatu fungsi f(x) disebut fungsi ganjil apabila berlaku f(–x) = –f(x) dan disebut fungsi genap apabila berlaku f(–x) = f(x). Jika f(–x) ≠ –f(x) maka fungsi ini bukan genap dan bukan ganjil. Untuk memahami fungsi ganjil dan fungsi genap, perhatikan contoh soal berikut ini.Contoh soal
Tentukan fungsi f di bawah ini termasuk fungsi genap, fungsi ganjil, atau tidak genap dan tidak ganjil.
1. f(x) = 6x3 + x
2. f(x) = cos x + 2
3. f(x) = 3x2 – x
Penyelesaian
1. f(x) = 6x3 + x
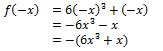
Jadi, fungsi f(x) merupakan fungsi ganjil.
2. f(x) = cos x + 2
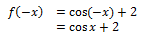
f(x) = –f(x)
Jadi, fungsi f(x) merupakan fungsi genap.
3. f(x) = 3x2 – x
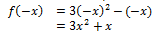
Fungsi f(–x) ≠ f(x) dan f(–x) ≠ –f(x).
Jadi, fungsi f(x) adalah tidak genap dan tidak ganjil.
selain fungsi-fungsi di atas masih ada beberapa fungsi yang lain, namun pembahasan kami hari ini cukup sekian dulu. Semoga bermanfaat
Relasi dan Fungsi
Relasi
Relasi adalah suatu aturan yang memasangkan anggota himpunan satu ke himpunan lain. Suatu relasi dari himpunan A ke himpunan B adalah pemasangan atau korespondensi dari anggota-anggota himpunan A ke anggota-anggota himpunan B.Jika diketahui himpunan A = {1, 2, 3, 4} dan B = {4, 5, 6, 7}, maka relasi “tiga kurangnya dari” himpunan A ke himpunan B dapat disajikan dalam diagram panah, diagram Cartesius, himpunan pasangan berurutan, dan dengan rumus.
a. Diagram panah
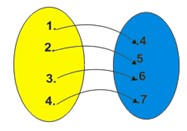
b. Diagram Cartesius
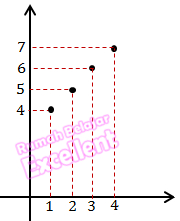
c. Himpunan pasangan berurutan
R = {(1,4), (2,5), (3,6), (4, 7)}
d. Dengan rumus
Relasi antara anggota himpunan A dan B dapat dinyatakan dengan menggunakan rumus. Misalnya anggota A dinyatakan dengan x, maka pasangannya, yaitu y merupakan anggota B, dirumuskan:
y = x + 3
atau dapat pula dinyatakan dalam bentuk
f(x) = x + 3, di mana x ∈ {1, 2, 3, 4}
Fungsi
Pengertian FungsiSuatu relasi dari himpunan A ke himpunan B disebut fungsi dari A ke B jika setiap anggota A dipasangkan dengan tepat satu anggota B.
Perhatikan diagram panah berikut.
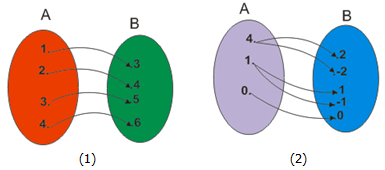
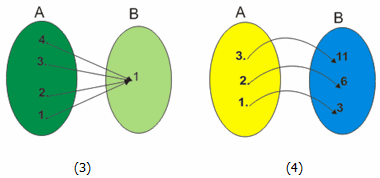
Pada gambar (1), (3) dan (4) di atas, setiap anggota himpunan A mempunyai pasangan tepat satu anggota himpunan B. Relasi yang memiliki ciri seperti itu disebut fungsi atau pemetaan. Sedangkan gambar (2) bukan fungsi karena ada anggota A yang punya pasangan lebih dari satu anggota B.
Jika f adalah suatu fungsi dari A ke B, maka:
- himpunan A disebut domain (daerah asal),
- himpunan B disebut kodomain (daerah kawan) dan
- himpunan C, yaitu anggota B yang berpasangan dengan himpunan A disebut range (hasil) fungsi f.
Untuk lebih memahami tentang fungsi, pelajarilah contoh soal berikut.
Diketahui A = {1, 2, 3, 4} dan B = {1, 2, 3, 4, 5, 6, 7, 8}.
Suatu fungsi f : A→B ditentukan oleh f(x) = 2x – 1.
1. Gambarlah fungsi f dengan diagram panah.
2. Tentukan domain, kodomain dan range fungsi f.
3. Gambarlah grafik fungsi f.
Penyelesaian:
Diketahui A = {1, 2, 3, 4}
f(x) = 2x – 1
x = 1 → f(1) = 2(1) – 1 = 1
x = 2 → f(2) = 2(2) – 1 = 3
x = 3 → f(3) = 2(3) – 1 = 5
x = 4 → f(4) = 2(4) – 1 = 7
a. Diagram Panah
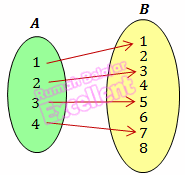
b. Dari diagram di atas terlihat bahwa
Domain: {1, 2, 3, 4}
Kodomain: {1, 2, 3, 4, 5, 6, 7, 8}
Range: {1, 3, 5, 7}
c. Grafik fungsi